| 4 minutes
If you’ve ever looked into product key algorithms, you’ve most likely heard of the algorithm Microsoft used in many products in the 90’s, most notably Windows 95. If you haven’t, it’s rather simple: the digit sum of a certain segment of the key must be divisible by seven.
But contrary to what some old writeups say, that’s not all there is to it. Let’s look at each key type that uses this algorithm, and see what other aspects make a key valid.
As a general note, the information provided here is designed to allow generating universally valid keys. However, I cannot possibly check every Microsoft product myself but I’m happy to be told of any missing rules, especially if they affect the universal nature of any mentioned example keys.
CD Keys
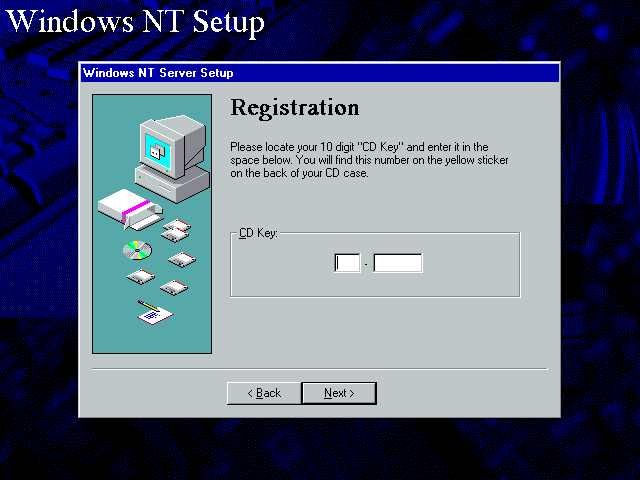
The CD key is the simplest type of key, which as the name implies came with retail CDs. It consists of two segments:
XXX - The first segment is the site number. It can be nearly anything from 000 to 998 (note that Windows 95 does not care about it being a number). The following site numbers are not allowed:
- 333
- 444
- 555
- 666
- 777
- 888
- 999
For maximum compatibility, always generate a number.
XXXXXXX - The second segment is where the algorithm comes into play. As mentioned earlier, the digit sum must be divisible by seven. The clever among you may have realised an obvious bug: 0 % 7 equals zero, which means that all zeroes pass the algorithm. This affects early users of the algorithm, notably Windows 95.
In later products such as NT 4 the last digit cannot be 0 or ≥ 8, this is a check digit rule which ends up preventing the all-zeroes bug, the reason for the ≥ 8 part is unknown. For maximum compatibility, implement this rule for any generated keys regardless of their type.
Based on these rules, the most basic universally valid key is 000-0000007. 111-1111111 is also commonly used.
At least Windows 95 is lax when it comes to the separator, and does not care what it is.
11-digit CD Keys
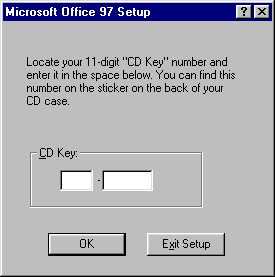
The 11-digit CD key is used by at least Office 97. Like regular CD keys, it consists of two segments:
XXXX - The first segment can be nearly anything from 0001 to 9991. There are no banned numbers, but the last digit much be 3rd digit + 1 or 2. When the result is > 9, it overflows to 0 or 1.
XXXXXXX - The second segment of the key is identical to regular CD keys without the check digit requirement (at least in Office 97).
Based on these rules, the most basic valid key that I’m comfortable recommending is 0001-0000007. 1112-1111111 also works, as expected.
OEM Keys
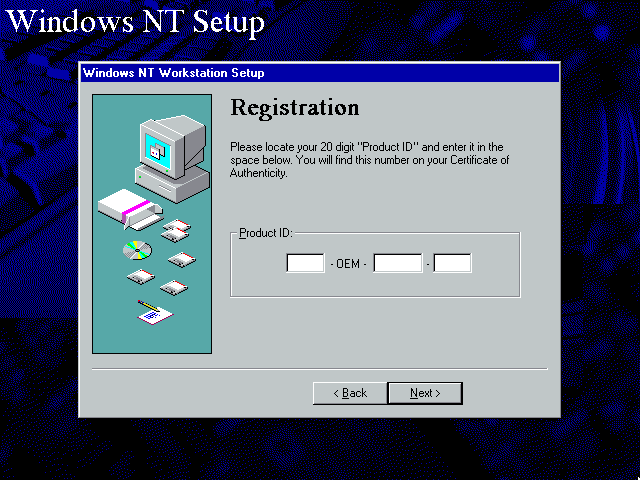
OEM keys are the most complex type of keys that use the mod7 algorithm, and typically came bundled with new computers. OEM keys consist of 4 segments:
XXXXX - The first segment represents the date the key was printed on. The first three digits can be anything from 001 to 366 (intended for leap years but that isn’t actually checked), and the last two are the year, anything from 95 to 03 (02 for Windows 95) is considered valid. For example, a key with 19296 as the first segment was printed on the 10th of July 1996. For maximum compatibility, cap the year value to 02 when generating.
OEM - The second segment is self-explanatory. The first Windows 95 release is the only piece of software I’m aware of that actually requires typing it in.
XXXXXXX - The third segment is where the algorithm comes into play again. The usual rule applies, except that the first digit must be 0 and the check digit rule must be followed.
XXXXX - The fourth segment is truly random, and can be anything numeric so long as it’s the correct length.
Based on these rules, the most basic valid key is 00100-OEM-0000007-00000. Highly mature people may want to forgo simplicity and go for 06900-OEM-0694207-80085 instead.
Conclusion
It isn’t as simple as one might expect to work with these keys, but at the same time all aspects of them could easily be guessed if you had valid keys to refer to.
I don’t think Microsoft intended this algorithm to be very robust, rather they just wanted a fast algorithm that kept the most basic software pirates at bay.
Sources used: The leaked Windows NT 4 source code, experimentation for 11-digit keys.
Errata:
- Exceptions for Windows 95 where not mentioned before (2021/02/09)
- The most basic valid key -> most basic universally valid key in CD keys section (2022/07/23)
- The obvious bug with the basic modulo check present in early versions of the algorithm was not mentioned at all, added generation hints, explicitly mention OEM keys needing the check digit (2024/09/30, bug noted by chungy in the 86Box community)